
定义损失函数:
定义激活函数:
前向传播
第一层(输入层):
加权和:
第二层(隐层):
加权和:
第三层(输出层):
计算误差值:
总结:要是使误差值最小,就需要误差反向传播算法,更新得到最小误差的权重参数w和b。
反向传播
须知:我们需要反向传递回去更新每一层对应的权重参数w和b。
我们使用链式法则来反向模式求导。
更新第三层(输出层)的权重参数:
更新参数w:
更新参数b:
同理可得:w4:也就是同一层的w都可以用这种方式更新。
更新上一层(隐层)的权重参数:
更新权重参数w和b:
其中:
同理可得:
综合上式:
更新:
同理可得:w2:也就是同一层的w都可以用这种方式更新。
推广
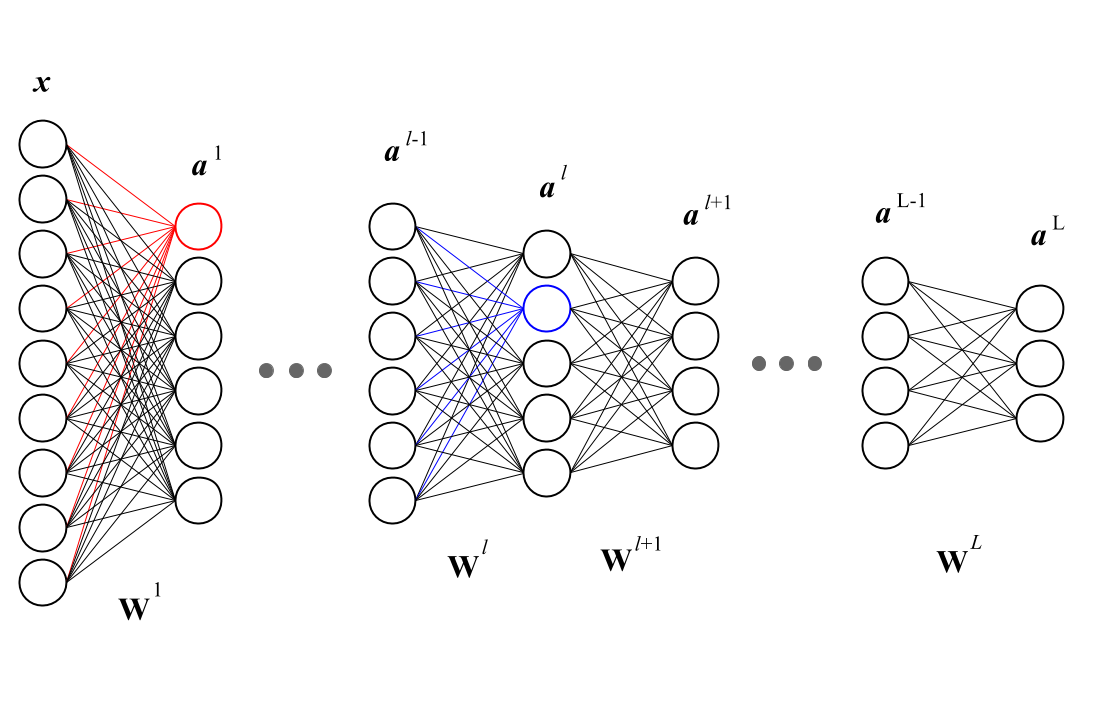
我们定义第L层的第i个神经元更新权重参数时(上标表示层数,下标表示神经元):
表示第l层的第i个神经元连接第l−1层的第j的神经元的相连的权重参数w。如下图所示:
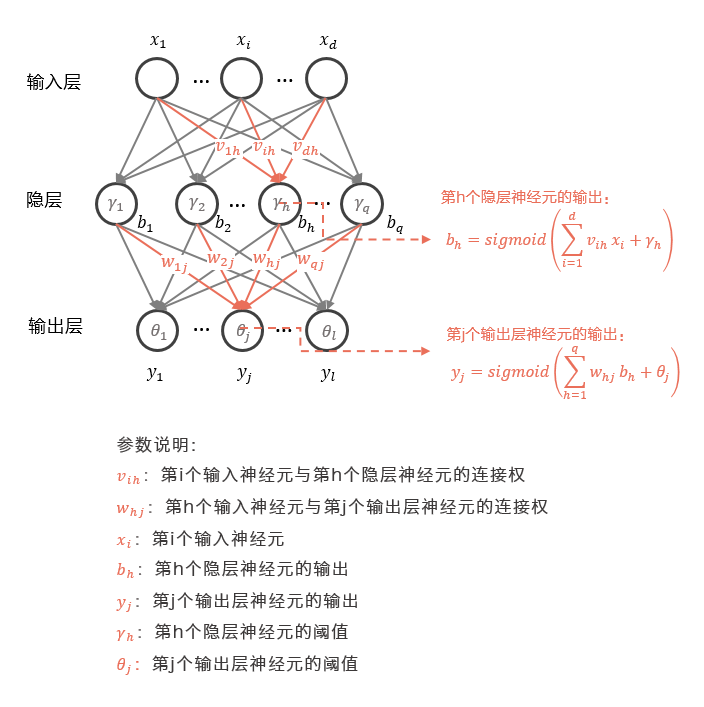
推广总结
根据前面所定义的:
对于第ll层:
对于偏置项bias:
四项基本原则
基本形式
矩阵形式
其中 ⨀是Hadamard乘积(对应位置相乘)
实例
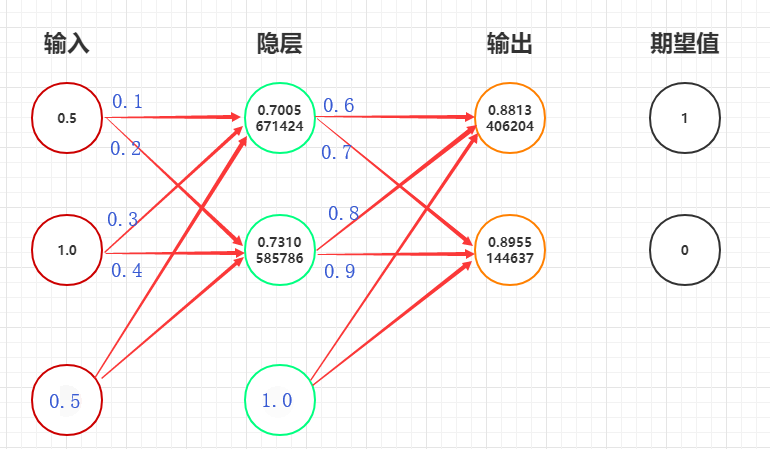
因为:
所以:
因为:
所以:
权重更新:
权重初始化
